순차 탐색
순차 탐색(Sequential Search)이란 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다.


순차 탐색은 이름처럼 순차로 데이터를 탐색한다.
순차 탐색은 정말 자주 사용되는데, 리스트에 특정 값의 원소가 있는지 체크할 때도 순차 탐색으로 원소를 확인하고, 리스트 자령에서 특정한 값을 가지는 원소의 개수를 세는 count() 메서드를 이용할 때도 내부에서는 순차 탐색이 수행된다.
#순차탐색
def sequential_search(n, target, array):
#각 원소를 하나씩 확인하며
for i in range(n):
if array[i] == target:
return i+1 #현재 위치 반환(인덱스는 0부터 시작하므로 1 더하기)
input_data = input().split()
n= int(input_data[0]) #원소의 개수
target = input_data[1] # 찾고자하는 문자열
array = input().split()
#순차탐색 수행 결과 출력
print(sequential_search(n, target, array))순차 탐색의 최악의 경우 시간 복잡도는 O(N)이다.
이진 탐색
이진 탐색(Binary Search)은 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다.
이진 탐색은 탐색 범위를 절반씩 좁혀가며 데이터를 탐색해야되는 특징이 있다.
이진탐색은 위치를 나타내는 변수 3개를 사용하는데 탐색하고자 하는 범위의 시작점, 끝점, 그리고 중간점이다.
찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는다.
다음은 이미 정렬된 데이터 10개의 데이터 중에서 값이 4인 원소를 찾는 예시이다.


이진 탐색은 한 번 확인할 때마다 확인하는 원소의 개수가 절반씩 줄어든다는 점에서 시간 복잡도가 O(logN)이다.
이진 탐색을 구현하는 방법에는 2가지가 있는데 하나는 재귀함수를 이용하는 방법이고, 하나는 단순 반복문을 이용하는 방법이다.
📌 재귀함수로 구현한 이진 탐색
#이진 탐색(재귀)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
#찾은 경우 중간점 인덱스를 반환
if array[mid] ==target:
return mid
#중간점의 값보다 찾는 값이 작은 경우 => 왼쪽확인
elif array[mid] > target:
return binary_search(array, target, start, mid-1)
#중간점의 값보다 찾는 값이 큰 경우 => 오른쪽확인
elif array[mid] < target:
return binary_search(array, target, mid+1 , end)
n, target = list(map(int, input().split()))
array = list(map(int, input().split()))
#결과 출력
result = binary_search(array, target, 0, n-1)
if result is None:
print("원소 존재하지 않음")
else :
print(result+1)
📌 반복문으로 구현한 이진 탐색
#이진 탐색(반복)
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end)//2
#찾은 경우 중간점 인덱스를 반환
if array[mid] ==target:
return mid
#중간점의 값보다 찾는 값이 작은 경우 => 왼쪽확인
elif array[mid] > target:
end = mid -1
#중간점의 값보다 찾는 값이 큰 경우 => 오른쪽확인
else:
end = mid +1
return None
n, target = list(map(int, input().split()))
array = list(map(int, input().split()))
#결과 출력
result = binary_search(array, target, 0, n-1)
if result is None:
print("원소 존재하지 않음")
else :
print(result+1)
이진탐색을 구현한 코드는 겉보기엔 쉬워보일 수 있으나, 아무런 참고코드 없어 스스로 온전히 작성하기에는 상당히 어려운 작업이 될 수 있다. 하지만 이진탐색은 코딩 테스트에서 단골로 나오는 문제이니 가급적 외우는걸 권장한다고 한다.(나동빈님이...)
더불어 코딩 테스트의 이진 탐색 문제는 탐색 범위가 큰 상황에서의 탐색을 가정하는 문제가 많다. 따라서 탐색 범위가 2000만을 넘어가면 이진 탐색으로 문제에 접근해보는것이 좋다. 처리해야 할 데이터의 개수나 값이 1000만 단위 이상으로 넘어가면 이진 탐색과 같이 O(logN)의 속도를 내야하는 알고리즘을 떠올려야 문제를 풀 수 있는 경우가 많다는 점을 기억하자.
트리 자료구조
이진 탐색은 전제조건이 데이터 정렬이다.
데이터베이스는 내부적으로 대용량 데이터 처리에 적합한 트리 자료구조를 이용하여 항상 데이터가 정렬되어 있다. 따라서 데이터베이스에서의 탐색은 이진탐색과는 조금 다르지만, 이진 탐색과 유사한 방법을 이용해 탐색을 항상 빠르게 수행하도록 설계되어 있어서 데이터가 많아도 탐색하는 속도가 빠르다.
트리 자료구조는 노드와 노드의 연결로 표현하며 노드는 정보의 단위로서 어떠한 정보를 가지고 있는 개체로 이해할 수 있다. 최단 경로에서는 노드가 '도시'와 같은 정점의 의미를 가진다고 하였다.
트리 자료구조는 그래프 자료구조의 일종으로 데이터베이스 시스템이나 파일 시스템과 같은 곳에서 많은 양의 데이터를 관리하기 위한 목적으로 사용한다.
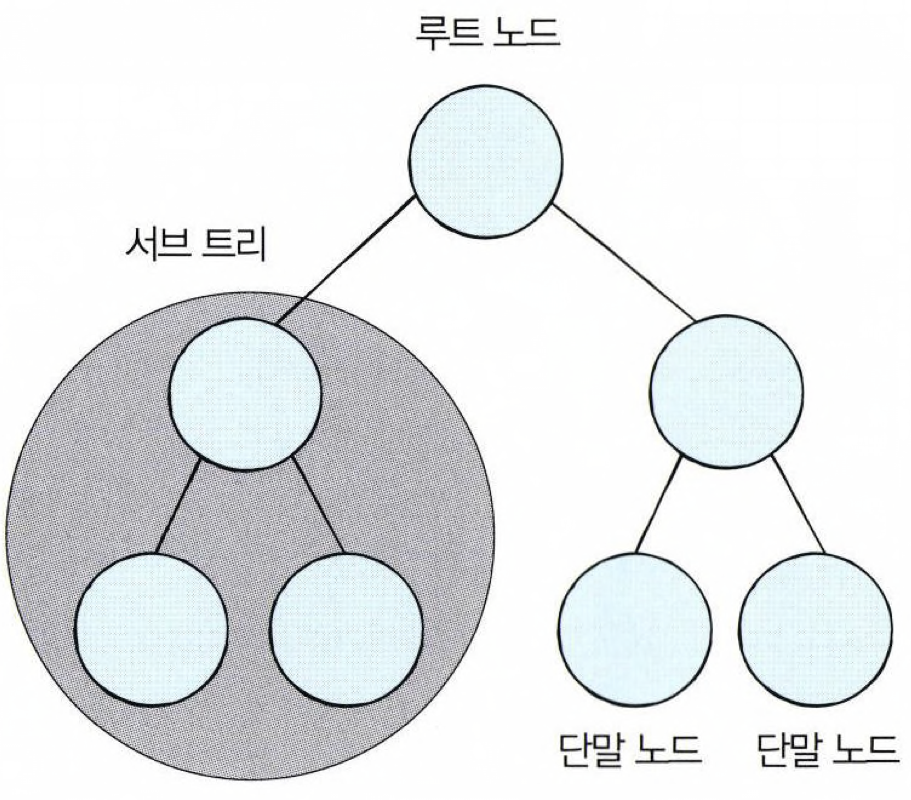
트리의 특징은 다음과 같은 것들이 있다.
- 트리는 부모 노드와 자식 노드의 관계로 표현된다.
- 트리의 최상단 노드를 루트 노드라고 한다.
- 트리의 최하단 노드를 단말 노드라고 한다.
- 트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리라 한다.
- 트리는 파일 시스템과 같이 계층적이고 정렬된 데이터를 다루기에 적합하다.
이진 탐색 트리
트리 자료구조 중에서 가장 간단한 형태가 이진 탐색 트리이다.

이진 탐색 트리는 다음과 같은 특징을 가진다.
- 부모 노드보다 왼쪽 자식 노드가 작다.
- 부모 노드보다 오른쪽 자식 노드가 크다.
- 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드


실전문제


정답👇🏻👇🏻👇🏻(더보기를 눌러주세용)
#부품 찾기, 솔아답안
def binary_search(arr, target, start, end):
if start > end:
return None
mid = (start + end) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
return binary_search(arr, target, mid+1, end)
else :
return binary_search(arr, target, start, mid-1)
n = int(input())
a = list(map(int, input().split()))
a.sort() #사전 정렬
m = int(input())
b = list(map(int, input().split()))
b.sort() #사전 정렬
for i in range(len(b)):
if binary_search(a, b[i], 0, len(a)-1):
print("yes", end=' ')
else :
print("no", end=' ')
먼저 매장 내 N개의 부품을 번호 기준으로 정렬하자. 그 이후에 M개의 찾고자 하는 부품이 각각 매장에 존재하는지 검사하면 된다.
이진 탐색 말고도 계수 정렬의 개념을 이용하여 문제를 풀 수도 있다.
#부품 찾기(계수 정렬 이용)
cmp = [0]*1000001
n = int(input())
a = list(map(int, input().split()))
for aa in a:
cmp[aa] += 1
m = int(input())
b = list(map(int, input().split()))
for bb in b:
if cmp[bb] != 0:
print("yes", end=' ')
else:
print("no", end=' ')
<이진탐색 풀이의 경우>
부품을 찾는 과정에서 최악의 경우 시간 복잡도 O(M x logN)의 연산이 필요하므로 이론상 최대 약 200만 번의 연산이 이루어진다고 분석할 수 있다. 오히려 N개의 부품을 정렬하기 위해 요구되는 시간 복잡도 O(N x logN)이 이론적으로 최대 약 2,000만으로 더욱더 많은 연산이 필요한 것을 알 수 있다.
결과적으로 이진 탐색을 사용하는 문제 풀이 방법의 경우 시간 복잡도는 O((M+N) x logN)이다.

정답👇🏻👇🏻👇🏻(더보기를 눌러주세용)
#떡볶이 떡 만들기
n, m = map(int, input().split())
arr = list(map(int,input().split()))
#이진 탐색을 위한 시작점과 끝점 설정
a= 0
b= max(arr)
result = 0
while a <= b:
total = 0
mid = (a+b) // 2
for i in range(n):
if arr[i] >= mid:
total += arr[i] - mid
if total < m: #잘린떡의 길이가 m보다 작을때
b = mid-1
else :
result = mid
a = mid+1
print(result)절단기의 높이 (탐색 범위)는 1부터 10억까지의 정수 중 하나인데, 이처럼 큰 수를 보면 당연하다는 듯이 가장 먼저 이진 탐색을 떠올려야 한다.이 문제에서 절단기의 높이 범위가 한정적이었다면 순 차 탐색으로 해결할 수 있지만, 현재 문제에서 절단기의 높이는 최대 10억까지의 정수이므로 순차 탐색은 분명 시간 초과를 받을 것이다.
반면에 높이 H를 이진 탐색으로 찾는다면, 대략 31번 만에 경우의 수를 모두 고려할 수 있다. 이때 떡의 개수 N이 최대 100만 개이므로 이진 탐색으로 절단기의 높이 H를 바꾸면서, 바꿀 때마다 모든 떡을 체크하는 경우 대략 최대 3,000만 번 정도의 연산으로 문제를 풀 수 있다.
시간제한은 2초이므로 최악의 경우 3,000만 번 정도의 연산이 필요하다면 아슬하게 시간초과를 받지 않고 정답 판정을 받을 것이다.
% 해당 글은 "이것이 코딩테스트다. (나동빈 저)" 를 공부하며 정리해놓은 게시글입니다! %
'CS+PS > Algorithm' 카테고리의 다른 글
| [알고리즘] 다이나믹 프로그래밍(DP) (1) | 2023.11.28 |
|---|---|
| [파이썬]빠른 입출력 (0) | 2023.11.13 |
| [알고리즘] 정렬 (선택, 삽입, 퀵정렬..) (0) | 2023.11.13 |
| [알고리즘] BFS/DFS (feat. stack, queue) (1) | 2023.10.11 |
| [C++] 연결리스트 (feat.바킹독) (0) | 2023.09.19 |



