Pixel2Mesh: Generating 3D Mesh Models from Single RGB Images
Nanyang Wang1 ⋆, Yinda Zhang2 ⋆, Zhuwen Li3 ⋆, Yanwei Fu4, Wei Liu5, Yu-Gang Jiang1 †
1 Shanghai Key Lab of Intelligent Information Processing, School of Computer Science, Fudan University
2 Princeton University
3 Intel Labs
4 School of Data Science, Fudan University
5 Tencent AI Lab
Abstract.
이 논문은 단일 컬러 이미지로부터 3D 형상을 삼각형 메쉬(triangular mesh) 형태로 생성하는 종단 간(end-to-end) 딥러닝 아키텍처를 제안한다. 이전의 방법들은 주로 3D 형상을 볼륨(volume) 또는 포인트 클라우드(point cloud) 형태로 표현했으나, 이러한 형식을 실제 사용 가능한 메쉬 모델로 변환하는 것은 쉽지 않다.
그래서 이 논문에서 제안하는 방법의 주요 특징은 다음과 같다.
1. 그래프 기반 컨볼루션 신경망(Graph-based Convolutional Neural Network) 사용
: 기존 방법과 달리, 이 네트워크는 3D 메쉬를 그래프 기반 컨볼루션 신경망으로 표현하여, 올바른 형상을 생성한다. 이 과정에서 입력 이미지에서 추출한 지각적 특징(perceptual features)을 활용한다.
2. 점진적인 변형(progressive deformation)
: 초기 형상인 타원체(ellipsoid)를 점진적으로 변형하는 방식으로, 형상이 안정적으로 변형될 수 있도록 거칠게 시작해서 점점 세밀하게(coarse-to-fine) 변화시키는 전략을 채택했다.
3. 메쉬 관련 손실 함수(mesh-related losses) 정의
: 여러 수준에서 메쉬의 시각적 매력과 물리적 정확성을 보장하기 위해 다양한 손실 함수를 설정했다.
4. 높은 3D 형상 추정 정확도
: 다양한 실험을 통해 이 방법이 더 높은 세부 표현력을 가진 메쉬 모델을 생성할 뿐 아니라, 기존 최첨단 기술들에 비해 3D 형상 추정 정확도가 높음을 보여준다.
Introduction

3D 형상을 추론하는 것이 인간에게는 자연스러운 기능이지만, 컴퓨터 비전에서는 매우 어려운 과제이다.
최근에는 단일 컬러 이미지에서 3D 형상을 생성하는 데 딥러닝 기술이 사용되어 좋은 성과를 내고 있지만, 기존 방법들은 3D 형상을 볼륨(volume)이나 포인트 클라우드(point cloud) 형태로 표현하는 데 그치고 표현 세부 정보를 잃어버리는 단점이 있다.
이 논문에서는 단일 이미지로부터 3D 삼각형 메쉬를 추출하는 새로운 알고리즘을 제안한다. 이 접근 방식은 단순히 메쉬를 생성하는 것이 아니라, 평균 형상에서 목표 형상으로 점진적으로 변형하는 방식을 사용한다. 이 방식의 장점은 다음과 같다 :
1. 잔여 변형(residual deformation) 을 예측하는 것이 구조화된 출력을 예측하는 것보다 신경망 학습에 더 효과적임
2. 여러 변형 단계를 통해 점진적으로 세밀하게 형상 다듬을 수 있음
3. 초기 메쉬에 대한 사전 지식(prior knowledge) 을 인코딩할 수 있어 다양한 형상에 적합함
특히, 이 논문에서는 토폴로지가 고정된 타원체(ellipsoid)(구멍이 없는 폐쇄형 메쉬 구조)를 변형하여 차량, 비행기, 테이블과 같은 일반적인 객체의 형상을 효과적으로 다룰 수 있음을 보여준다.
이 논문에서 해결해야 할 주요 과제는 다음과 같다 :
1. 메쉬 모델 표현 방법
: 메쉬는 본질적으로 불규칙한 그래프 구조이므로, 2D 이미지에서 추출한 특징을 효과적으로 통합하기 위해서는 두 데이터 형태(2D 이미지와 3D 그래프) 간의 정보 융합이 필요 => 이를 위해 1) graph-based fully convolutional network (GCN) 를 사용하여 메쉬 모델의 각 꼭짓점(vertex) 을 노드로 표현하고, 인접 노드 간 특징 교환을 통해 3D 위치를 회귀하는 방법을 채택했다. 2)VGG-16 유사 아키텍처를 통해 2D 이미지에서 특징을 추출한 뒤, 각 GCN 노드가 해당 2D 이미지 위치에서 특징을 풀링하도록 설계했다. (<- 이 부분에 대해서는 잘 이해하지 못했다...!) => 즉, VGG-16 은 딥러닝 모델로, 여러 층의 2D 합성곱(convolution) 과 풀링(pooling) 연산을 통해 입력 이미지의 고수준 특징을 추출한다. 이렇게 추출된 특징을 3D 메쉬 정점의 위치에 해당하는 이미지 정보와 결합하여 메쉬 변형 학습에 활용한다. 이렇게 되면 더 정확하고 세부적인 3D 객체를 생성할 수 있다.
2. 버텍스 위치 업데이트
: 직접 많은 버텍스를 예측하는 경우 오류가 발생할 수 있어, 그래프 언풀링(graph unpooling) 레이어를 도입하여 초기에는 적은 버텍스로 시작해 점진적으로 추가하면서 세부 정보를 추가하도록 설계했다. 이를 통해 네트워크가 보다 넓은 수용 영역을 가지고 학습할 수 있도록 했다. (<- 이 부분에 대해서 아직 잘 이해하지 못했다...! ) => 적은 버텍스로 시작하면 네트워크가 전체적인 글로벌 구조를 먼저 학습. 이후 세부적인 버텍스를 추가하면서 로컬 세부 사항을 점진적으로 학습.
3. 학습의 품질 향상
: 그래프 구조 덕분에 인접 노드 간 고차 손실 함수를 정의할 수 있어 3D 형상을 규제할 수 있다. 예를 들어, 표면 평활(smoothness) 손실, 엣지 균일화 손실, 라플라시안 손실을 정의하여 품질 좋은 메쉬 모델을 생성하도록 했다. (<- 이 부분에 대해서 아직 잘 이해하지 못했다...! )
Related Work
1. Multi-view geometry (MVG) 방법
- 주요 접근법 : Structure from Motion (SfM) 과 Simultaneous Localization and Mapping (SLAM).
- 제한 사항 :
- 여러 시점이 필요하여 보이지 않는 부분을 복원할 수 없고, 충분한 시점을 얻기 위해 시간이 오래 걸림
- 반사나 투명한 물체와 같은 비-램버시안(non-lambertian) 표면 및 텍스처가 없는 물체 복원에 어려움
- 이러한 한계 때문에 학습 기반 방법이 주목받기 시작함
2. 학습 기반 접근법
- 주로 단일 또는 소수의 이미지를 활용하고, 데이터로부터 형상 우선 지식을 학습함
- 딥러닝 구조와 대규모 데이터셋(예: ShapeNet) 덕분에 연구가 크게 진전됨
3. 학습 기반 접근법의 주요 기법
- 형상 검색 및 변형 : Huang 등과 Su 등이 데이터셋에서 형상 구성 요소를 검색해 이미지를 맞추기 위해 변형함. 그러나 이 접근은 해결하기 어려운 ill-posed 문제임
- 3D 변형 가능 모델 : Kar 등은 범주별 3D 변형 모델을 제안했으나, 인기 있는 범주에 한정되며 세부 표현이 부족함
- 복셀 기반 복원 : 대부분의 딥러닝 방법은 3D 복셀을 사용하지만, GPU 메모리 제약으로 인해 해상도가 낮음. Tatarchenko 등은 옥트리(octree) 표현을 통해 더 높은 해상도를 제공함
- 포인트 클라우드 : Fan 등은 포인트 클라우드를 생성하지만, 포인트 간 연결이 없어 3D 메쉬 복원에 바로 사용하기 어려움
- 지오메트리 이미지 : 일부 연구는 3D 형상을 나타내기 위해 2D 합성곱 신경망을 이용한 "지오메트리 이미지"를 사용함
4. 최근 연구 및 한계
- 실루엣 기반 방법과 대규모 모델 저장소를 사용하는 결합 모델 생성 방법이 관련 연구로 제시되었으나, 복잡한 형상에서는 성능이 저조하거나 많은 자원을 요구함
5. 그래프 신경망(Graph Neural Network, GNN) 을 활용한 3D 복원
- 본 연구는 그래프 신경망(GNN) 을 기반으로 형상 분석을 수행하며, 최근 형상 분석 GNN이 적용된 연구에서 영감을 받음
- 차팅 기반 방법 : 메쉬 객체에 적합한 표면 다양체에 합성곱을 적용하는 방법으로, 단일 이미지 3D 복원에는 많이 사용되지 않았음
Method
Preliminary: Graph-based Convolution
1. 3D 메쉬 구성
: 3D 메쉬는 정점(Vertices), 간선(Edges), 면(Faces) 으로 이루어진 구조이다.
그래프로 표현할 수 있으며, M= (V, E, F) 로 나타낸다.

그래프의 각 정점 (Vertex) 에서는 특성(feature) 벡터가 할당된다.
2. 그래프 기반 합성곱 (Graph-based Convolution)
: 불규칙한 그래프 상의 합성곱 층을 정의하며, 식(1) 과 같이 나타낼 수 있다.


위의 특성 업데이트 식의 핵심 : 정점 p의 특성은 자기 자신의 특성(w0fp^l)과 이웃 정점의 특성 합(w1 fq^l)의 선형 결합으로 업데이트
위의 연산을 통해 정점의 특성을 업데이트하며, 이는 메쉬의 변형(deformation)을 적용하는 것과 유사한 효과를 낸다.
3. 특성 벡터
: 정점에 연결된 특성 벡터 fp는 3D 정점 좌표, 3D 형상 특징 인코딩, 입력 컬러 이미지에서 학습된 특징(존재할 경우)의 결합으로 구성된다.
=> 이러한 합성곱은 메쉬의 형상을 유지하며, 복잡한 구조에서도 효과적으로 작동하도록 설계되었다.
System Overview
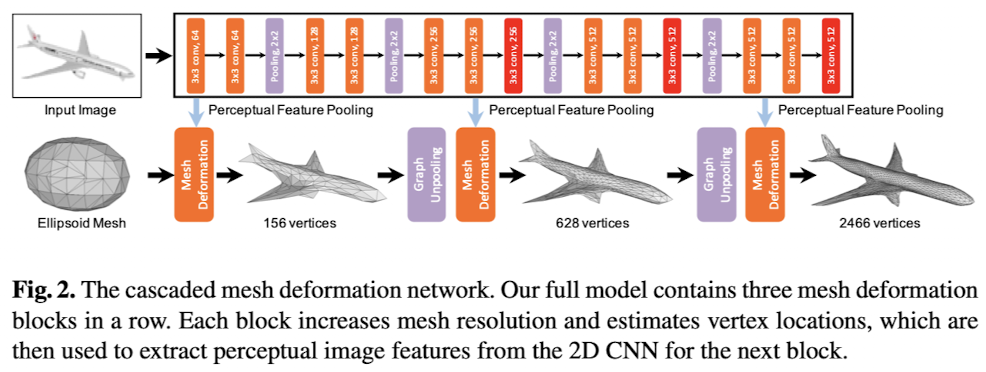
<Fig 2> 이 모델은 세 개의 메쉬 변형 블록(Mesh Deformation Network) 으로 구성되어 있다. 각 블록은 순차적으로 메쉬 해상도를 높이고 정점(vertex) 위치를 추정한다.
1) 변형 블록(Mesh Deformation) : 각 메쉬 변형 블록은 이전 단계에서 추정된 정점 위치를 기반으로 메쉬의 해상도를 높인다.
2) 특징 추출 : 추정된 정점 위치를 사용하여 2D CNN으로부터 이미지의 지각적(perceptual) 특징을 추출한다. 이 특징은 다음 변형 블록에서 메쉬 변형을 더 정교하게 수행하기 위한 입력으로 활용된다.
=> 즉, 각 블록은 메쉬의 해상도를 높이고, 이를 기반으로 2D CNN 에서 더 정확한 특징을 추출해 다음 변형 블록의 입력으로 사용하는 구조이다. 이를 통해 모델은 점진적으로 고해상도의 정교한 3D 메쉬를 생성한다.
이 논문의 모델은 단일 컬러 이미지를 입력으로 받아 3D 메쉬 모델을 생성하는 엔드투엔드 딥러닝 프레임워크이다.
1. 구성
- 전체 네트워크는 이미지 특징 네트워크와 계층적 메쉬 변형 네트워크로 구성된다.
- 이미지 특징 네트워크는 2D CNN으로, 입력 이미지에서 특징을 추출한다. 이 특징은 메쉬 변형 네트워크에서 메쉬를 원하는 3D 모델로 변형하는 데 사용된다.
2. 메쉬 변형 네트워크
- 그래프 기반 합성곱 네트워크(GCN) 로, 세 개의 변형 블록(Mesh Deformation) 과 두 개의 Graph unpooling 층이 교차로 배치되어 있다.
- Mesh Deformation은 현재의 메쉬 모델을 나타내는 그래프를 입력으로 받아 새로운 정점 위치와 특징을 생성한다.
- Graph unpooling 층은 세부 표현을 위해 정점 수를 늘리면서 삼각형 메쉬 구조를 유지한다.
3. 작동 방식
- 모델은 소수의 정점에서 시작해, 점차적으로 메쉬를 변형하고 세부사항을 추가하는 방식으로 작동한다.
4. 손실 함수
- Chamfer Distance 손실 외에 Surface normal 손실, Laplacian 정규화 손실, Edge length 손실을 추가하여 안정적인 변형과 정확한 메쉬 생성을 유도한다.
Initial ellipsoid
이 모델은 사전 3D 모양에 대한 지식 없이 초기 타원체(ellipsoid)로부터 변형을 시작한다.
초기 타원체의 특징은 다음과 같다.
- 카메라 좌표에서 평균 크기로 설정된 타원체가 사용되며, 카메라 앞쪽 0.8 미터 지점에 배치된다. 타원체의 세 축은 각각 0.2m, 0.2m, 0.4m 의 반지름을 가진다.
- 초기 메쉬 생성: Meshlab의 암묵적 표면 알고리즘(Implicit surface algorithm) 을 사용해 타원체의 메쉬 모델을 생성하며, 이 모델은 156개의 정점(Vertices) 으로 구성된다.
초기 타원체는 네트워크의 입력 그래프로 사용되며, 정점의 3D 좌표만을 포함한 초기 특징이 할당된다. 이후, 이 타원체는 네트워크에서 점차 변형되어 원하는 3D 모양으로 만들어진다.
Mesh deformation block
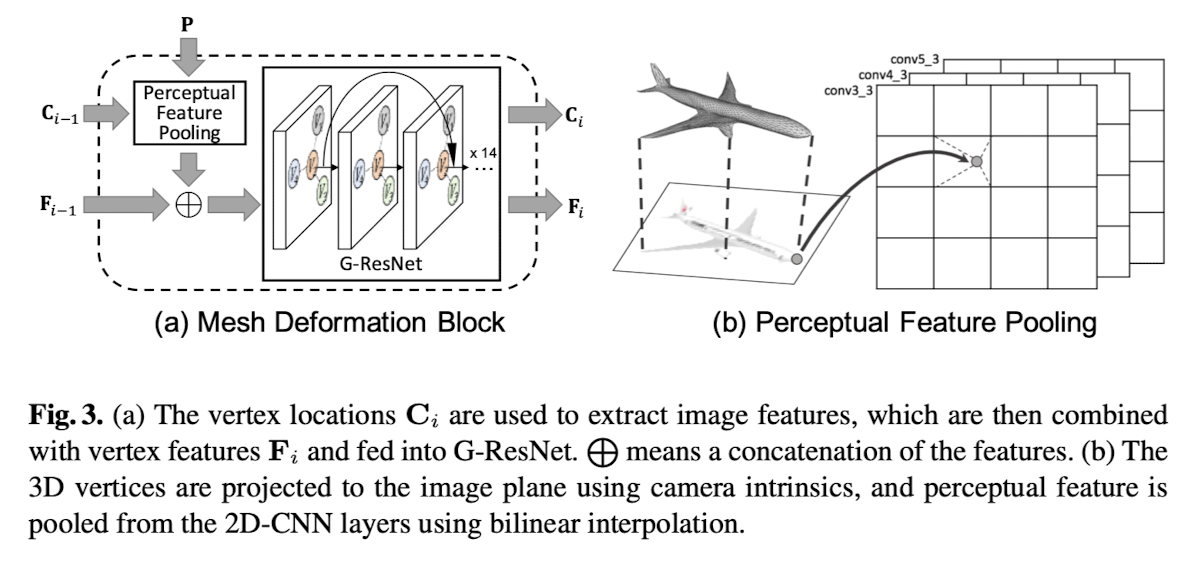
<Fig 3>
(a) Mesh Deformation Block
1. 정점 위치 Ci-1 : 현재 메쉬 모델의 정점 위치이다. 이 위치는 이미지 특징을 추출하기 위해 사용된다.
2. Perceptual Feature Pooling :
- 정점 위치 Ci-1 를 사용해, 카메라 내부 파라미터로 2D 이미지 평면에 투영한다.
- VGG-16 네트워크의 conv3_3, conv4_3, conv5_3 레이어에서 특징을 추출하고, 이 특징들은 쌍선형 보간법(bilinear interpolation)을 통해 풀링
* Bilinear interpolation 이란?
2D 공간에서 값을 예측하기 위해 주변의 네 개의 인접한 점을 사용하여, 가중합으로 새로운 값을 계산하는 보간법이다. 이름에서 알 수 있듯이, 두번의 선형 보간(linear interpolation)을 거쳐 값을 계산한다. 이는 특히 이미지 처리에서, 픽셀 값을 확대하거나 줄일 때 자주 사용된다.
사용하는 이유
- 정점(Vertex)의 위치가 이미지 위에서 정확히 픽셀의 중앙에 위치하지 않을 수 있다. 이 경우, 해당 위치의 특징 값을 추출하기 위해 주변 네 개의 픽셀 값을 사용한다.
- 쌍선형 보간법은 이 네 픽셀 값의 가중합을 계산해, 정확한 위치에서의 특징 값을 얻는 방법이다.
3. Vertex Features Fi-1 :
- 이전 블록에서 전달된 3D 정점 특징이다.
- 풀링된 perceptual feature 와 함께 연결(concaternate, 그림에서 +에 동그라미 되어있는 기호) 되어 G-ResNet의 입력으로 사용된다.
4. G-ResNet :
- Graph-based ResNet 구조로, 14개의 그래프 잔차(Residual) 컨볼루션 레이어로 이루어져 있다.
- 입력 특징을 기반으로 새로운 정점 위치 Ci 와 새로운 정점 특징 Fi를 생성한다.
(b) Perceptual Feature Pooling
- 3D 메쉬의 정점들이 카메라 내부 파라미터를 사용해 2D 이미지 평면에 투영된다.
- VGG-16의 conv3_3, conv4_3, conv5_3에서 추출된 이미지를 기반으로 주변 픽셀의 특징을 쌍선형 보간법으로 풀링한다.
- 풀링된 perceptual feature 는 정점의 3D 특징과 결합되어 G-ResNet에 입력된다.
자 이제, Fig3에 대해서 살펴 보았으니 주요 단계를 살펴보도록 하자.
1. 이미지 특징 추출 및 풀링 :
- 입력 이미지에서 특징을 추출하기 VGG-16 네트워크(conv5_3 레이어까지 사용)를 활용한다.
- 정점(vertex)의 3D 좌표를 기반으로 이를 카메라 내부 파라미터를 이용해 2D 이미지 평면으로 투영한다.
- 투영된 좌표를 중심으로 주변 4개의 픽셀로부터 쌍선형 보간법(bilinear interpolation) 을 통해 이미지를 풀링한다.
- 이 풀링 단계에서는 conv3_3, conv4_3, conv5_3 레이어에서 추출된 특징을 연결(concatenate)하며, 총 1280차원의 이미지 특징이 생성된다.
2. 정점 특징 결합 :
- 풀링된 이미지 특징은 입력 메쉬의 3D 특징(128차원)과 연결되어, 총 1408차원의 특징 벡터가 생성된다.
- 첫 번째 블록에서는 초기 학습된 3D 특징이 없기 때문에, 3D 좌표만 연결하여 사용한다. (3차원)
3. G-ResNet (Graph-based ResNet) :
- 1408차원 특징 벡터는 G-ResNet으로 전달된다. G-ResNet은 깊은 그래프 기반 잔차 신경망으로, 각 정점의 새로운 위치와 3D 특징을 예측한다.
- G-ResNet 은 14개의 그래프 잔차 컨볼루션 레이어로 구성되어 있으며, 각 레이어는 128 채널을 가진다.
- 이 네트워크는 정점 간의 정보 교환을 효율적으로 수행하도록 설계되었다. 기본적인 그래프 컨볼루션은 이웃 정점 간의 정보 교환만 가능하기 때문에, 네트워크의 깊이를 깊게 하고 shortcut connections을 추가하여 수용 영역 문제(receptive field issue) 를 해결한다.
- 마지막 레이어에서는 추가 그래프 컨볼루션 레이어를 적용하여 각 정점의 새로운 3D 좌표를 출력한다.
* 수용 영역이란 ?
네트워크가 한 정점에서 정보를 얻을 수 있는 다른 정점 들의 수를 뜻한다.
기본적인 그래프 컨볼루션에서는 각 정점이 직접적으로 이웃한 정점들과만 정보를 교환할 수 있다. 이로 인해 네트워크의 깊이가 증가함에 따라 정보의 전파 범위가 늘어나지 않거나, 너무 많은 층을 쌓으면 그로 인한 정보 손실이 발생할 수 있다. 이는 수용 영역의 문제로, 깊이가 깊어지거나 복잡해질수록 각 정점이 참조할 수 있는 정보 범위가 한정되어, 더 넓은 범위의 정보를 효율적으로 처리하기 어려워지는 문제이다.
이 문제를 해결하기 위해 shortcut connections나 네트워크의 깊이를 증가시켜 수용 영역을 활장하려는 접근이 필요하다. 이렇게 하면 더 멀리 떨어진 정점들의 정보를 빠르게 교환할 수 있어 네트워크의 학습 성능이 향상된다.
여기서 궁금한점 : 네트워크의 깊이가 증가하면 정보의 범위가 늘어나지 못한다는 말은 어떻게 해석할 수 있을까?
=> 기본적으로, 그래프 컨볼루션 네트워크에서는 각 레이어가 인접한 정점들과만 정보를 교환하므로, 네트워크의 깊이가 늘어가면 정보가 전파되는 범위는 늘어나긴한다, 하지만 문제는 깊이가 깊어질수록 정보가 점차 소실되거나 왜곡될 수 있다는 점이다. 이는 네트워크의 여러 층을 통과하면서 정보가 점차 희석되거나, 멀리 있는 정점들과의 관계를 잘 파악하지 못하게 되는 현상이다.
Shortcut connections(또는 skip connections)를 추가하는 이유는 이 문제를 해결하기 위해서이다. 네트워크의 깊이가 깊어질수록 각 층을 건너뛰어 정보를 전달하는 경로를 추가함으로써, 깊이가 증가하더라도 정보가 사라지지 않도록 도와준다. 즉, shortcut connections는 정보를 더 잘 보존하고, 네트워크의 깊이를 늘리면서도 정보가 왜곡되지 않도록 한다.
Graph unpooling layer

<Fig 4>
(a) Graph Unpooling
- 검은색 정점과 점선 엣지는 unpooling 과정에서 새로 추가된 정점과 엣지를 나타낸다.
- Face-based 방법 : 삼각형(face)의 중심에 새로운 정점을 추가하고, 이 정점을 기존 삼각형의 세 정점과 연결한다. 하지만 이 방식은 정점의 차수(degree)가 불균형해지는 문제를 야기할 수 있다.
- Edge-based 방법 : 엣지의 중앙에 새로운 정점을 추가하고, 이 정점을 엣지의 양 끝 정점들과 연결한다. 추가적으로, 같은 삼각형 내에서 추가된 세 정점은 서로 연결되어 새로운 삼각형이 만들어진다. 이 방식은 정점의 차수가 더 균일하게 유지되도록 도와준다.
(b) Comparison between Face-based and Edge-based Unpooling
- inital Mesh : Unpooling 이 적용되기 전의 초기 메시 구조이다. 상대적으로 적은 수의 정점과 삼각형으로 구성되어 있다.
- Face-based 방법 : 정점의 차수가 불균형해져 불규칙적인 구조가 나타난다.
- Edge-based 방법 : 정점의 차수가 균등하게 유지되며, 더 균일하고 규칙적인 구조를 형성한다.
Unpooling layer 는 정점 수를 효율적으로 증가시키는 방법으로, 처음에 적은 수의 정점으로 시작하고 필요에 따라 정점을 추가하는 방식이다. 기존의 face-based 접근은 불균형한 정점 차수를 유발하는 반면, 엣지 기반 접근은 균형 잡힌 방식으로 정점을 추가하여 더 좋은 성능을 낸다. 이 방식은 컴퓨터 그래픽스에서의 메시 분할 알고리즘을 차용하여, 각 엣지의 중앙에 새로운 정점을 추가하고 이를 기존 정점들과 연결하여 정점의 수를 증가시키고, 메모리 효율성과 성능 개선을 동시에 추구한다.
Losses
메시 변형(Mesh deformation) 과정에서 출력 형태(output shape)의 특성과 변형 절차를 제약하기 위해 네 가지 손실 함수를 정의한다. => 예쁘고 자연스러운 결과를 보장하기 위해 다음과 같은 손실을 적용한다.
1. Chamfer loss

- Chamfer 거리는 두 점 집합(예측된 메시와 실제 메시)의 모든 점들 간의 거리를 측정하는 손실 함수이다.
- 이 수식은 다음 두 가지 부분으로 구성된다.
1. 예측된 메시의 정점 p 에서 실제 메시의 가장 가까운 정점 q 까지의 거리
2. 실제 메시의 정점 q에서 예측된 메시의 가장 가까운 정점 p 까지의 거리
- 이 손실은 예측된 메시의 정점들이 실제 메시의 정점들과 가까워지도록 유도한다.
=> 문제점 : Chamfer 손실은 정점 위치를 정확하게 예측하는 데는 유용하지만, 표면의 부드러움이나 고차원적인 특성을 잘 반영하지 못할 수 있다. 예를 들어, 메시의 세밀한 곡률(curvature) 정보나 표면 일관성을 반영하지 못하기 때문에, 단순히 정점이 근처에 있는 것 만으로는 고품질의 3D 메시를 생성하기 어렵다.
2. Normal loss


q : Chamfer 손실 계산 시, p 와 가장 가까운 실제 메시의 정점 q 이다.
k : p 의 이웃인 이웃 픽셀을 의미한다.
nq : ground truth 에서의 관측된 표면 법선이다.
Normal loss의 목적
- 이 손실 함수는 법선 방향을 기준으로 최적화를 진행하며, 특히 정점 p 의 이웃 정점과의 간격과 법선 방향의 일관성을 맞추려고 한다.
- 구체적으로는 p 와 k 사이의 벡터가 ground truth 에서 주어진 법선(nq) 과 수직이 되도록 최적화하려고 한다.
- "수직" 이라는 말은, p 와 k 간의 벡터가 ground truth의 표면 법선 벡터와 내적값이 0에 가까워지도록 한다는 말이다.
- 최적화 과정에서는 표면의 접선 평면을 잘 맞추는 방향으로 학습이 이루어지며, 이 손실은 미분 가능하여 학습 과정에서 유용하게 사용된다.
💡 Back propagation
“이 손실은 미분 가능하여 학습 과정에서 유용하게 사용됩니다”라는 표현은 백프로파게이션(Backpropagation)과 관련 있다.
-> Back propagation 은 신경망에서 오차 역전파 방법을 사용하여 가중치를 업데이트하는 알고리즘이다. 이 과정에서 손실 함수의 미분값을 계산하여 가중치가 최적화될 수 있도록 돕는다.
-> 미분 가능하다는 것은 손실 함수가 연속적이고 기울기를 계산할 수 있는 함수라는 뜻이고, 손실 함수의 미분값은 네트워크의 가중치(혹은 파라미터)가 어떻게 변경되어야 하는지를 알려주는 중요한 정보이다.
-> 만약 손실함수가 미분 가능하지 않다면, 기울기를 계산할 수 없어 백프로파게이션을 사용할 수 없게 된다. 따라서 모델의 학습이 어려워지거나 불가능할 수 있다.
3. Regularization
문제 : Local Minimum
- Chamfer loss 와 Normal loss 를 사용해도, 3D 메쉬 모델이 국소 최소값에 갇혀서 최적화가 제대로 이루어지지 않을 수 있다.
특히, 초기 추정이 실제 값에서 멀리 떨어져있을때(즉, 네트워크가 잘못된 결과를 출력할 때) 과도한 변형(deformation) 이 발생할 수 있으며, 이는 vertex 가 비정상적으로 이동(flying vertices) 하는 문제를 초래할 수 있다.
Laplacian Regularization
- Laplacian regularization은 정점(vertex) 들이 너무 자유롭게 이동하는 것을 방지하는 기법이다. 이렇게 하면 메쉬 모델이 자기 교차(self-intersection)를 일으키는 문제를 예방할 수 있다.
- 이 정규화 기법은 이웃 정점(neighboring vertices) 들이 동일한 방식으로 움직이도록 유도하여 세부사항을 보존하는 역할을 한다.
- 처음에는 (첫 번째 변형 블록에서) 표면이 평평한 타원체로 입력되므로 표면의 매끄러움을 유지하는 역할을 하며, 이후 블록에서는 너무 과도한 변형을 방지하며 미세한 세부사항만 추가하도록 돕는다.
- Laplacian 좌표는 각 정점 p에 대해 정의되며, 이 좌표는 이웃 정점들 간의 평균 위치와 비교하여 변형 전후의 차이를 측정한다.

- Laplacian 정규화 손실은 다음과 같이 정의된다. 여기서 프라임값과 그냥 값은 변형 전과 후의 Laplacian 좌표이다.

Edge Length Regularization
- Flying vertices 문제는 보통 긴 간선(long edge) 을 유발하는데, 이 문제를 해결하기 위해 edge length regularization 을 도입한다.
- 이 손실은 이웃 정점들 간의 간격이 지나치게 커지는 것을 방지하여 메쉬 모델이 과도하게 변형되지 않도록 한다. 간선 길이에 대한 정규화 손실은 다음과 같이 정의된다.

최종 손실 함수(Overall Loss)
- 최종 손실 함수는 여러 손실 함수들의 가중합(weighted sum) 으로 구성된다. 각 손실 항목에는 가중치가 할당되어 있으며, 이를 통해 네트워크가 학습 과정에서 각 손실 항목의 중요도를 조절할 수 있다.
- 이와 같이 여러 정규화 기법을 함께 사용하여, 안정적이고 자연스러운 3D 메쉬 변형을 유도할 수 있다.


Experiment
Data.
데이터 출처 : 이전 논문 Choy et al. 에서 제공한 ShapeNet (3D CAD 모델들의 대규모 데이터셋) 데이터셋 이용
데이터 구성 : 50,000개의 3D CAD 모델, 13개의 객체 카테고리가 있음(예: car, chair, airplane)
렌더링 이미지 : 각 3D CAD 모델은 다양한 카메라 관점(viewpoint) 에서 2D 이미지로 렌더링
Evaluation Metric.
1. F-Score :
- 정밀도(precision)와 재현율(Recall)의 조화 평균(harmonic mean)
- 계산 과정
- 결과(예측값)와 실제값(ground truth)에서 점(point)을 샘플링
- 각 샘플링된 점에 대해 상대방(ground truth 또는 예측)의 Nearest Neighbor 을 찾는다.
- 특정 임계값 tau 내에 상대방의 점이 있다면 매칭 성공으로 간주한다.
- Precision : 예측 된 점들 중 얼마나 많은 점이 실제 값의 점과 매칭되었는지를 나타낸다.
- Recall : 실제 값의 점들 중 얼마나 많은 점이 예측된 점과 매칭되었는지를 나타낸다.
- 값이 클수록 좋음
2. Chamfer Distance (CD):
- 두 점 집합(예측과 실제) 간의 평균 점 거리
- 두 점 집합 간의 전반적인 유사성 평가
- 값이 작을수록 좋음
3. Earth Mover's Distance (EMD):
- 두 점 집합 간의 전반적인 유사성 평가
- 값이 작을수록 좋음
기존 지표의 한계 : 기존 지표들은 점 간 거리나 점유 상태에 중점을 둠. 그러나, 표면 품질(surface properties)와 같은 고차원 특성(예: continuity, smoothness, high-order details)을 반영하지 못함.
Baselines (비교 대상 모델).
1. 3D-R2N2 (Choy et al., 2016):
- 입력 이미지에서 3D 볼륨(Volume)을 생성하는 방식
- 복셀 기반 출력으로, 3D 형태를 표현하지만 해상도가 낮아 세부사항 표현이 제한적
- 제안된 방법과 비교하려면, Marching Cube 알고리즘을 통해 복셀을 메쉬로 변환해야 함.
2. PSG (Fan et al., 2017):
- 입력 이미지에서 포인트 클라우드(Point Cloud)를 생성하는 방식
- 포인트 클라우드는 3D 공간의 점들로 객체를 표현하며, 세부사항 표현은 가능하지만 표면 구조가 부족할 수 있음
- 평가 지표가 포인트 클라우드에 정의되어 있으므로 PSG의 출력은 직접 평가 가능
3. Neural 3D Mesh Renderer (N3MR, 2018):
- 입력 이미지에서 메쉬(Mesh)를 생성하는 딥러닝 기반 모델
- 코드가 공개된 유일한 메쉬 생성 모델로, 기존 방식과 직접적인 비교 가능
모든 모델이 동일한 데이터셋으로 학습되었고, 동일한 학습/테스트 데이터 분할을 사용.
모든 모델이 동일한 학습 시간으로 훈련되어 비교의 공정성 확보
1. 포인트 클라우드 기반 평가:
- 모든 모델의 출력을 포인트 클라우드로 변환하여 동일한 기준에서 평가
2. 왜 포인트 클라우드로 평가하나?
- Chamfer Distance(CD), Earth Mover’s Distance(EMD)와 같은 평가 지표는 포인트 클라우드에서 정의된다.
Training and Runtime.
1. 학습 설정:
- 입력 이미지: 224 x 224
- 초기 메쉬: 156개의 정점, 462개의 간선으로 구성된 초기 타원체(Ellipsoid)
- 구현 환경: TensorFlow
- 최적화 방법: Adam Optimizer 사용, Weight Decay(1 * 10^-5 의 가중치 감쇠를 사용하여 과적합 방지)
- 배치 크기 : 1
- 학습 스케줄 : 학습 에포크(50), 초기 학습률(3 * 10^-5), 학습률 감소(40번째 에포크 이후, 학습률 1 * 10^-5 낮춰 안정적인 최적화 유도)
- 총 학습 시간: NVIDIA Titan X GPU를 사용하여 72시간
2. 실행 성능:
- 테스트 시 메쉬 생성 속도: 2466개의 정점 생성에 평균 15.58ms
Comparison to state of the art

F-score (Tab. 1)
제안된 모델의 성능:
- 대부분의 카테고리에서 Ours 는 모든 방법보다 높은 F-score를 기록
- 특히, 작은 임계값 tau 에서 다른 모델에 비해 최소 10% 높은 F-score를 보인다.
- 작은 tau 에서 우수하다는 것은 세부적인 정밀도를 잘 복원했음을 의미한다.
예외:
- Watercraft 카테고리에서 다른 모델에 뒤쳐짐.
N3MR의 성능:
- 약 50% 낮은 성능을 기록.
- 원인: N3MR은 이미지의 실루엣 신호(silhouette signal)만 학습하며, 3D 메쉬를 명시적으로 처리하지 않기 때문이다.
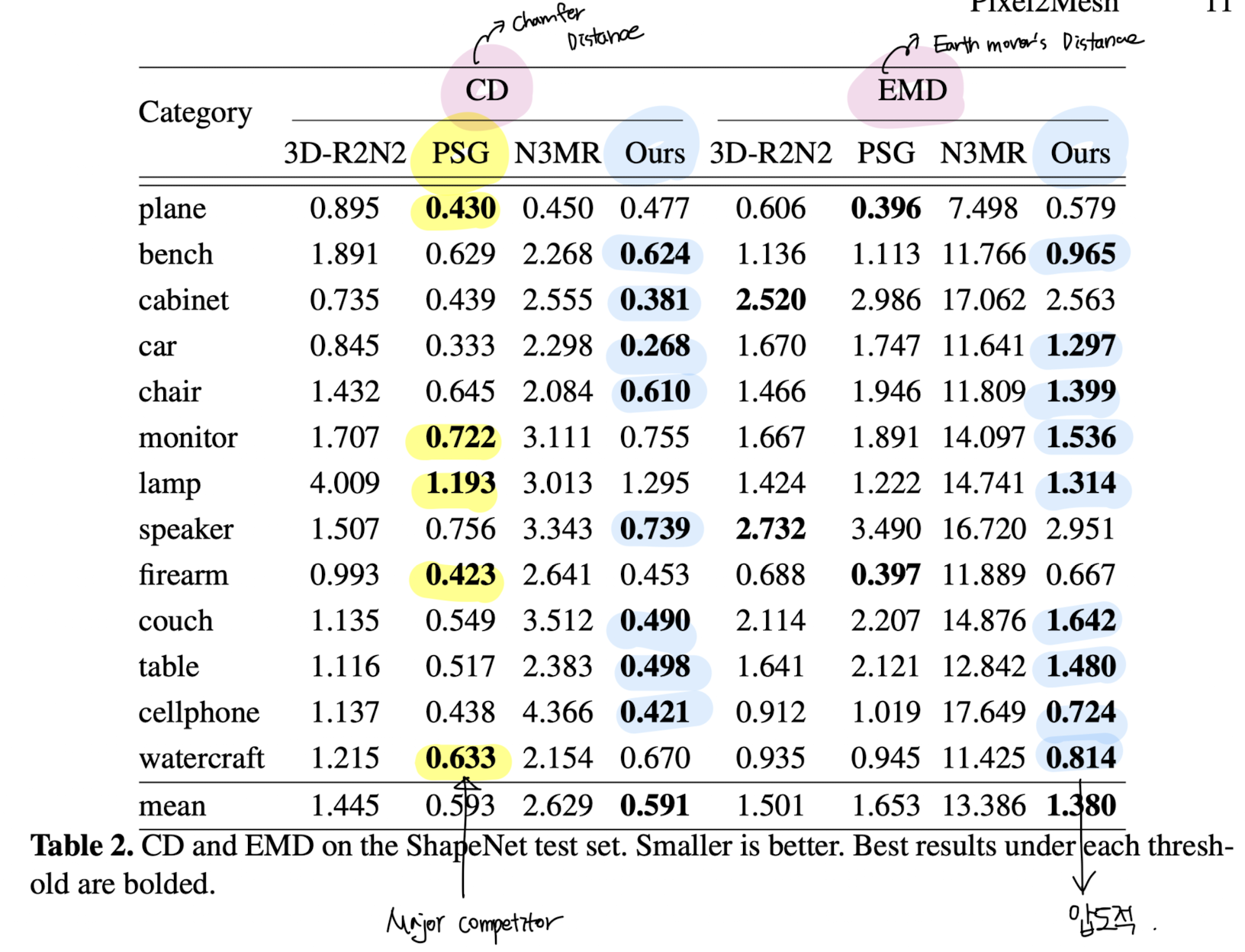
CD와 EMD (Tab. 2)
제안된 모델의 성능:
- 대부분의 카테고리에서 가장 낮은 CD와 EMD를 기록하며, 최고 평균 점수(0.591)
PSG와의 비교:
- PSG는 포인트 클라우드 기반으로 자유도가 높아 CD와 EMD에서 더 낮은 값을 얻는 경우가 있음
- 그러나, 이 자유도는 적절한 정규화가 없으면 메쉬 모델 품질에 부정적인 영향을 미침

정성적 결과 분석 (Fig. 8)
다른 모델들의 한계
1. 3D-R2N2:
- 낮은 해상도로 인해 디테일 부족
- 예: 의자 다리와 같은 세부 사항이 복원되지 않음
- Octree 기반 해결 시도: 해상도를 증가시키려 했으나, 표면 디테일 복원이 여전히 어려웠다
2. PSG:
- 희소한 포인트 클라우드를 생성
- Chamfer loss가 회귀 손실처럼 작동하여 자유도가 너무 높아 메쉬 복원이 어려움
3. N3MR:
- 매우 거친 형태를 생성: 단순 렌더링 작업에는 충분할 수 있으나, 의자, 테이블과 같은 복잡한 객체 복원에는 부적합
제안된 모델의 장점
1. 메쉬 표현:
- 메쉬 구조를 사용하여 해상도에 제한되지 않음
- 메모리 제한을 극복하며 매끄러운 표면과 지역적 세부 사항(local details)을 포함
2. 지각적 특징 통합:
- 입력 이미지의 Perceptual Feature를 효과적으로 활용하여 세부 사항 복원
3. 학습 과정에서 정교하게 정의된 손실:
- Chamfer loss, Normal loss, Laplacian regularization 등 적절한 손실 함수 설계로 안정적인 학습 유도
Ablation Study (성분 분석 실험)
Ablation Study 는 딥러닝, 머신러닝, 또는 시스템 설계에서 특정 요소를 제거하거나 변경한 후, 결과를 비교하여 각 요소의 중요성을 분석하는 연구 방법이다.


<정량적 평가의 한계>
- Tab. 3에 따르면 엣지 길이 정규화(Edge Length Regularization) 를 제거한 모델이 F-score, CD, EMD에서 가장 높은 성능을 보임
- 그러나, Fig. 5에서 확인한 시각적 품질은 가장 나쁜 메쉬를 생성함
- 예: 메쉬가 비정상적으로 왜곡되거나, flying vertices 문제가 발생
<정성적 평가의 중요성>
- 정량적 지표는 점 간 거리나 점유 상태만 측정하며, 메쉬의 시각적 품질(예: 매끄러운 표면, 디테일 보존)을 반영하지 못한다
- Fig. 5의 시각적 결과를 통해, 각 구성 요소가 3D 메쉬 품질을 개선하는 데 어떻게 기여하는지 확인 가능
<제거된 요소>
1. Graph Unpooling
- Graph Unpooling Layers를 제거하여, 모든 블록에서 정점(vertex) 수가 동일하게 유지되도록 설정
- 이는 기존의 점진적으로 정점을 추가하는 방식(Coarse-to-Fine)을 사용하지 않는 구조를 의미.
- 결과:
- 초기 단계에서 변형(Deformation) 과정에서 오류 발생 가능성 증가:
- 초기 오류가 후속 블록에서 수정되지 못함.
- 결과적으로, 객체의 일부 영역에서 눈에 띄는 왜곡(artifacts)이 발생.
- 의의: Graph Unpooling은 정점을 점진적으로 추가하면서 변형 과정을 세밀하게 조정할 수 있게 해주므로, 모델의 안정적 학습에 필수적
2. G-ResNet (Shortcut Connections)
- G-ResNet에서 Shortcut Connection(Residual Connection)을 제거하여 일반적인 Graph Convolutional Network(GCN)으로 변경
- 결과:
- 모든 평가 지표(Tab. 3)에서 성능이 크게 감소: Chamfer Distance 최적화 실패
- 원인:
- 2D CNN에서도 관찰된 Degradation Problem(성능 퇴화 문제):
- 너무 깊은 네트워크는 학습이 어려워져 학습 오류(training error)가 증가하고, 테스트 오류(testing error)도 증가
- 제안된 모델은 42개의 Graph Convolutional Layers를 가지므로, 이 문제의 영향이 더욱 두드러진다
- 의의:
- Shortcut Connection은 기울기 소실 문제를 해결하고, 깊은 네트워크에서도 학습 안정성을 제공
- G-ResNet에서 Shortcut Connection은 3D 메쉬 복원 과정의 핵심 구성 요소임
3. 손실 함수(Loss Terms)
A. Normal Loss 제거
- 결과:
- 표면의 매끄러움(Smoothness)과 지역적 디테일(Local Details)이 심각하게 손상
- 예: 의자 등받이(seat back)의 세부 사항이 사라짐
- 의의:
- Normal Loss는 표면의 법선 방향을 유지하여 매끄러운 표면과 세부 사항 복원을 돕는 중요한 역할
B. Laplacian Term 제거
- 결과:
- Geometry Self-Intersection(기하학적 교차)가 발생
- 예: 의자 손잡이(handheld)가 교차하거나 잘못된 형태를 가짐
- 의의:
- Laplacian Term은 정점의 국소적인 구조(topology)를 유지하고, 안정적인 변형을 가능하게 함
C. Edge Length Term 제거
- 결과:
- Flying Vertices와 비정상적으로 긴 간선(edge)이 생성되어 표면이 망가짐
- 예: 메쉬 표면 전체가 제대로 형성되지 못함
- 의의:
- Edge Length Term은 정점 간의 간격을 조정하여 메쉬의 연결성을 유지하고, 표면 왜곡을 방지
Number of Deformation Blocks
Deformation Block 이란?
- Deformation Block은 초기 메쉬(Ellipsoid) 에서 시작하여 메쉬를 점진적으로 변형시키는 단계이다.
- 각 블록은 정점과 간선을 증가시키고, 새로운 세부 사항을 추가하여 3D 메쉬의 해상도를 높인다.

위의 왼쪽 그림을 보면 블록의 개수가 증가할수록 F-score 가 상승하고 Chamfer Distance 가 감소하여 성능이 향상됨을 보여준다.
하지만, 블록 개수가 3에서 4로 증가할 때는 성능 향상이 거의 포화 상태(Saturated) 임을 관찰할 수 있다.
블록 개수가 증가하면 정점과 간선 수가 많아져서 메쉬가 더욱 세밀하게 만들어질 수 있다. 하지만 속도와 효율성, 계산 시간과 복잡도가 크게 증가하므로 본 논문에서는 블록 수 3을 선택했다.
Reconstructing Real-World images

- 제안된 모델은 Synthetic Data (합성 데이터) 인 ShapeNet에서 학습되었다.
- 모델을 Real-World images(실제 이미지) 에서 테스트할 때 추가적인 fine-tuning 없이, 학습된 상태 그대로 사용하였다.
- 결과 : 실제 데이터에서도 강력한 성능을 보였다.
Conclusion
- 제안된 접근법은 단일 이미지로부터 고품질의 3D triangular mesh 를 생성하는데 성공적이었다.
<네트워크 설계>
- 네트워크 구조:
- 매우 깊은(cascaded) 그래프 합성곱 신경망(Graph Convolutional Neural Network) 설계
- Shortcut Connections(잔차 연결)를 통해 학습 안정성과 성능을 향상
- 메쉬 정밀화 과정:
- 네트워크는 Chamfer Loss와 Normal Loss로 엔드 투 엔드(end-to-end) 학습
- 메쉬를 단계적으로 정밀하게 개선.
- 메쉬 표현의 장점을 효과적으로 활용하며, 기존 SOTA 방식(3D Volume, 3D Point Cloud) 보다 더 나은 성능을 보였다.



